こんにちは、車いすテニス男子シングルスで国枝選手が金メダル獲得しましたね!強すぎました!かっこよかったです!!
さて、いよいよ明日2021年9月5日にQC検定の試験があります。今日も過去問やって90%近く正答できるようになりましたが、まだ何度出てきても対応できていないところがありますので、まとめて明日の試験本番に備えたいと思います。
無相関の検定
相関関係があるかどうかの検定を無相関の検定といいます。この無相関の検定で使う検定統計量は、
$$ t_0=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $$
ここで、rは相関係数、nはサンプル数です。
また棄却域は\( t(n-2,\alpha) \)で求められます。
二元配置実験の推定
①繰り返しのない場合、繰り返しありの交互作用を無視する場合
最適条件\(A_iB_j\)での点推定:
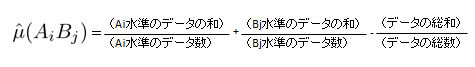
信頼率\( (1-\alpha) \)での信頼区間:
$$\hat{\mu}(A_iB_j) \pm t(\phi_E, \alpha)\sqrt{\frac{V_E}{n_e}} $$
ここで、\( \phi_E\)は誤差Eの自由度(繰り返しありの場合は\(\phi_{E’}\)、\( V_E\)は誤差の平均平方、\(n_e\)は有効繰り返し数(有効反復数)と呼ばれ、
$$ \frac{1}{n_e}=\frac{1}{m}+\frac{1}{l}-\frac{1}{lm} $$
ここでmはA水準数、lはB水準数、lmはA水準\(\times\)B水準。
②繰り返しありで交互作用を無視しない場合
最適条件\( A_iB_j\)での点推定:
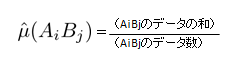
信頼率\( (1-\alpha) \)での区間推定:
$$ \hat{\mu}(A_iB_j) \pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{r}} $$
で表されます。ここで、\(\phi_E\)は誤差Eの自由度、\(V_E\)は誤差の平均平方、rは\(A_iB_j\)のデータ数。
まとめ
以上です!何度やってもできなかったところをまとめて整理することで不安が少し解消されました!
明日ベストを尽くして合格を手にしてきます!
めいり


コメント