こんにちは、今日過去問やったら全体で76%とれていました!本番2週間前から平日は毎朝4時過ぎに起きて仕事前に2時間勉強できている効果が出ているようでうれしかったです。ですが、まだまだ計算の分野が6割ちょっとしかないので最後まで頑張ります。
今回は計数値に用いる管理図の中心線、管理限界線の求め方をまとめたいと思います。
前回計量値に用いる管理図の中心線、管理限界線の求め方をまとめましたのでこちらをご覧ください↓
計数値に用いる管理図
前回も使いましたが管理図の種類をまとめてみました。
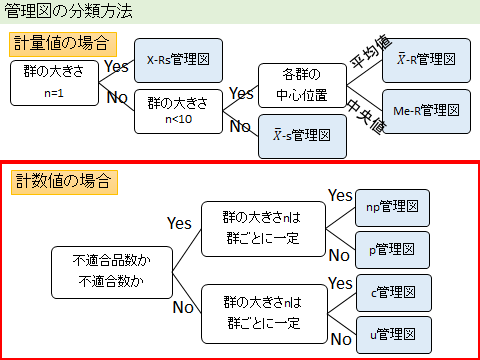
今回は上の図でも赤色で囲った計数値の場合をまとめていきます。np管理図、p管理図、c管理図、u管理図の4つありますので1つずつまとめていきます。
np管理図
サンプル中に不良品が何個あったかという不良個数npで工程を管理するときに用いられます。ただし、サンプルの大きさnが一定の場合のみです。
中心線について
$$ \rm{CL}=n\overline{p}=\frac{\sum np}{k} $$
で求められます。ここでnpは不良個数、kは群の数を表しています。
管理限界線について
上方管理限界線
$$ \rm{UCL}=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})} $$
下方管理限界線
$$ \rm{LCL}=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})} $$
で求められます。ここで、工程平均不良品率\( \overline{p}\)は、
$$ \overline{p}=\frac{\sum np}{\sum n} $$
です。
p管理図
p管理図は不良率pの管理図です。np管理図とは違い、サンプルの大きさnは一定でなくても使用できます。
中心線について
$$ \rm{CL}=\overline{p}=\frac{\sum np}{\sum n} $$
です。ここで、npはサンプル中の不良個数、nは1群のサンプルサイズです。全体の不良率が中心線になるんですね。
管理限界線について
上方管理限界線
$$ \rm{UCL}=\overline{p}+3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} $$
下方管理限界線
$$ \rm{LCL}=\overline{p}-3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} $$
c管理図
欠点数の管理図です。サンプルの大きさが一定のときに用いられます。
中心線について
$$ \rm{CL}=\overline{c}=\frac{\sum c}{k} $$
ここで\( \overline{c}\)は工程平均欠点数、cは欠点数、kは群の数です。
管理限界線について
上方管理限界線
$$ \rm{UCL}=\overline{c}+3\sqrt{\overline{c}} $$
下方管理限界線
$$ \rm{LCL}=\overline{c}-3\sqrt{\overline{c}} $$
になります。
u管理図
サンプル中の欠点数cをその単位当たりの欠点数uに直した管理図です。サンプルの大きさが一定でないです。
中心線について
$$ \rm{CL}=\overline{u}=\frac{\sum c}{\sum n} $$
です。ここでcは欠点数、nはサンプルの大きさです。
管理限界線について
上方管理限界線
$$ \rm{UCL}=\overline{u}+3\sqrt{\frac{\overline{u}}{n}} $$
下方管理限界線
$$ \rm{LCL}=\overline{u}-3\sqrt{\frac{\overline{u}}{n}} $$
で求められます。
まとめ
今回は計数値を用いる管理図(np管理図、p管理図、c管理図、u管理図)の中心線、管理限界線の求め方をまとめました。
前回の計量値を用いる管理図含めて管理図の要点を抑えました。
もし出題されたら確実に点数取れるようにまた演習します。
めいり

コメント